Blurring and Filtering images With OpenCV

by malabdalicomputer vision

2D Convolution ( Image Filtering )

As in one-dimensional signals, images also can be filtered with various low-pass filters (LPF), high-pass filters (HPF), etc. LPF helps in removing noise, blurring images, etc. HPF filters help in finding edges in images
OpenCV provides a function cv.filter2D() to convolve a kernel with an image.

Normalized Box Filter

To perform a smoothing operation we will apply a filter to our image. The most common type of filters are linear, in which an output pixel’s value .

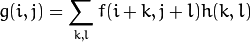
g(i,j) = \sum_{k,l} f(i+k, j+l) h(k,l)
kernel = Mat::ones(5, 5, CV_8UC);/25
dst = filter2D(img,-1,kernel)
//or
blur = blur(img,dest,5)

// or you can use boxFilter
filter2D(InputArray src, OutputArray dst, int ddepth, InputArray kernel, Point anchor=Point(-1,-1), double delta=0, int borderType=BORDER_DEFAULT )

Median Filter

The median filter run through each element of the signal (in this case the image) and replace each pixel with the median of its neighboring pixels

median.jpg
medianBlur ( src, dst, i );//i is kernal size

Gaussian Filter

  • Probably the most useful filter (although not the fastest). Gaussian filtering is done by convolving each point in the input array with a Gaussian kernel and then summing them all to produce the output array.
  • Just to make the picture clearer, remember how a 1D Gaussian
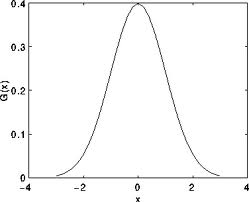
../../../../_images/Smoothing_Tutorial_theory_gaussian_0.jpg
  • Assuming that an image is 1D, you can notice that the pixel located in the middle would have the biggest weight. The weight of its neighbors decreases as the spatial distance between them and the center pixel increases.
gaussian.jpg

Gaussian Filter Generation

G(x, y)=\frac{1}{2\pi \sigma ^{2}}e^{-\frac{x^{2}+y^{2}}{2\sigma ^{2}}}
void FilterCreation(double GKernel[][5]) 
{ 
    // intialising standard deviation to 1.0 
    double sigma = 1.0; 
    double r, s = 2.0 * sigma * sigma; 
  
    // sum is for normalization 
    double sum = 0.0; 
  
    // generating 5x5 kernel 
    for (int x = -2; x <= 2; x++) { 
        for (int y = -2; y <= 2; y++) { 
            r = sqrt(x * x + y * y); 
            GKernel[x + 2][y + 2] = (exp(-(r * r) / s)) / (M_PI * s); 
            sum += GKernel[x + 2][y + 2]; 
        } 
    } 
  
    // normalising the Kernel 
    for (int i = 0; i < 5; ++i) 
        for (int j = 0; j < 5; ++j) 
            GKernel[i][j] /= sum; 
} 
0.00296902    0.0133062    0.0219382    0.0133062    0.00296902    
0.0133062    0.0596343    0.0983203    0.0596343    0.0133062    
0.0219382    0.0983203    0.162103    0.0983203    0.0219382    
0.0133062    0.0596343    0.0983203    0.0596343    0.0133062    
0.00296902    0.0133062    0.0219382    0.0133062    0.00296902

Bilateral Filter

  • So far, we have explained some filters which main goal is to smooth an input image. However, sometimes the filters do not only dissolve the noise, but also smooth away the edges. To avoid this (at certain extent at least), we can use a bilateral filter.
  • In an analogous way as the Gaussian filter, the bilateral filter also considers the neighboring pixels with weights assigned to each of them. These weights have two components, the first of which is the same weighting used by the Gaussian filter. The second component takes into account the difference in intensity between the neighboring pixels and the evaluated one.
bilateralFilter(InputArray src, OutputArray dst, int d, double sigmaColor, double sigmaSpace, int borderType=BORDER_DEFAULT )
Parameters:	
src – Source 8-bit or floating-point, 1-channel or 3-channel image.
dst – Destination image of the same size and type as src .
d – Diameter of each pixel neighborhood that is used during filtering. If it is non-positive, it is computed from sigmaSpace .
sigmaColor – Filter sigma in the color space. A larger value of the parameter means that farther colors within the pixel neighborhood (see sigmaSpace ) will be mixed together, resulting in larger areas of semi-equal color.
sigmaSpace – Filter sigma in the coordinate space. A larger value of the parameter means that farther pixels will influence each other as long as their colors are close enough (see sigmaColor ). When d>0 , it specifies the neighborhood size regardless of sigmaSpace . Otherwise, d is proportional to sigmaSpace .
bilateral.jpg